이번 장에서는 텍스트 형태의 코드를 컴파일 가능한 논리적 구조로 파싱하는 방법을 다룸
CPython은 코드를 파싱하기 위해 CST(concrete syntax tree)와 AST(abstract syntax tree) 두가지 구조를 사용
파싱 과정은 아래와 같음
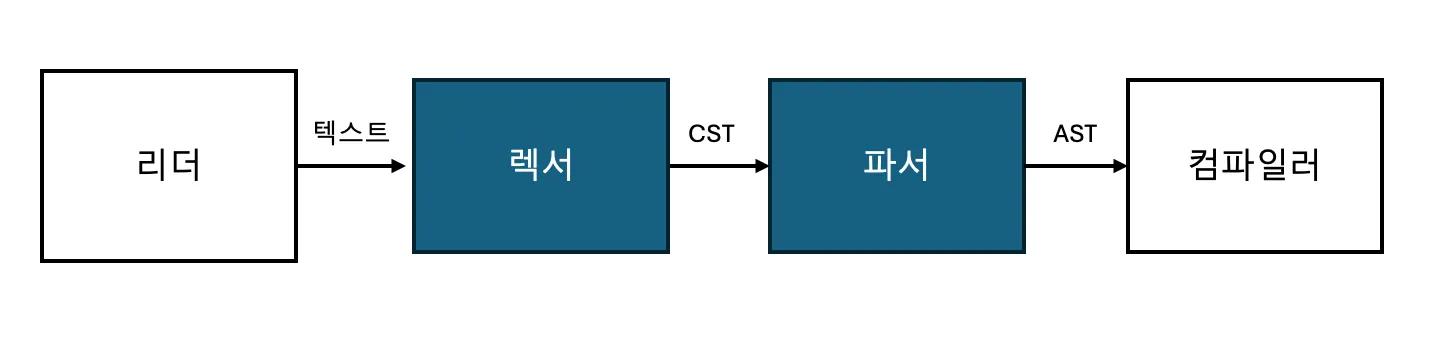
- 파서-토크나이저 또는 렉서(lexer)가 CST를 생성
- 파서가 CST로 부터 AST를 생성
6.1 CST 생성
- 파스 트리라고도 부르는 CST는 문맥 자유 문법에서 코드를 표현하는 루트와 순서가 있는 트리
- 토크나이저와 파서가 CST를 생성. 파서 생성기는 문맥 자유 문법이 가질 수 있는 상태에 대한 결정적 유한 오토마타 파싱 테이블을 생성
- CST에서 if_stmt같은 심벌은 분기로, 토큰과 단말 기호는 리프 노드로 표시
ex) 산술 표현식 a + 1 을 CST로 표현하면 아래와 같음

- 산술 표현식은 크게 좌측 항, 연산자, 우측항으로 나뉨
- 파서는 입력 스트미으로 들어오는 토큰들이 문법적으로 허용되는 토큰과 상태인지 확인하며 CST를 생성
- CST를 구성하는 모든 심벌은 Grammar/Grammar 파일에서 정의
# L147
arith_expr: term (('+'|'-') term)*
term: factor (('*'|'@'|'/'|'%'|'//') factor)*
factor: ('+'|'-'|'~') factor | power
power: atom_expr ['**' factor]
atom_expr: [AWAIT] atom trailer*
atom: ('(' [yield_expr|testlist_comp] ')' |
'[' [testlist_comp] ']' |
'{' [dictorsetmaker] '}' |
NAME | NUMBER | STRING+ | '...' | 'None' | 'True' | 'False')토큰은 Grammar/Tokens 파일에서 정의
ENDMARKER
NAME
NUMBER
STRING
NEWLINE
INDENT
DEDENT
LPAR '('
RPAR ')'
LSQB '['
RSQB ']'
COLON ':'
COMMA ','
SEMI ';'- NAME 토큰은 변수나 함수, 클래스 모듈의 이름을 표현
- 파이썬 문법에서 await이나 async 같은 예약어나 숫자 형식 또는 리터럴 타입 등은 NAME 값으로 쓸 수 없음
- 예를 들어, 함수 이름으로 1을 사용하려고 하면 SyntaxError가 발생
>>> def 1():
File "<python-input-0>", line 1
def 1():
^
SyntaxError: invalid syntaxNUMBER는 다양한 숫자 형식 값을 표현하는 토큰으로 다음과 같은 특수 문법들을 사용할 수 있음
- 8진수 값: 0o20
- 16진수 값: 0x10
- 이진수 값: 0b1000
- 복소수 값: 10j
- 부동 소수점 값: 1.01
- 밑줄로 구분된 값: 1_000_000
6.2 파서-토크나이저
- 렉서 구현은 프로그래밍 언어마다 다르고 렉서 생성기로 파서 생성기를 보완하는 언어도 있음
- CPython의 파서-토크나이저는 C로 작성되었음
6.2.1 연관된 소스 파일 목록
- Python/pythonrun.c : 파서와 컴파일러 실행
- Parser/parsetok.c : 파서와 토크나이저 구현
- Parser/tokenizer.c : 토크나이저 구현
- Parser/tokenizer.h : 토큰 상태 등의 데이터 모델을 정의하는 토크나이저 구현 헤더 파일
- Include/token.h : Tools/scripts/generate_token.py에 의해 생성되는 토큰 정의
- Include/node.h : 토크나이저를 위한 CST 노드 인터페이스와 매크로
6.2.2 파일 데이터를 파서에 입력하기
- 파서-토크나이저 진입점인 PyParser_ASTFromFileobject()는 파일 핸들과 컴파일러 플래그, PyArena 인스턴스를 받아 파일 객체를 모듈로 변환
파일을 2단계로 변환됨
- PyParser_ParseFileObject()를 사용해 CST로 변환
- AST 함수 PyAST_FromNodeObject()를 사용해 CST를 AST 또는 모듈로 변환
PyParser_ParseFileObject() 함수는 2가지 중요 작업을 수행
- PyTokenizer_FromFile()을 사용해 토크나이저 상태 tok_state를 초기화
- parsetok()을 사용해 토큰들을 CST(노드 리스트)로 변환
6.2.3 파서-토크나이저의 흐름
- 커서가 텍스트 입력의 끝에 도달하거나 문법 오류가 발견될 때까지 파서와 토크나이저를 실행
// Parser/parsetok.c L164
node *
PyParser_ParseFileObject(FILE *fp, PyObject *filename,
const char *enc, grammar *g, int start,
const char *ps1, const char *ps2,
perrdetail *err_ret, int *flags)
{
struct tok_state *tok; // (1)
if (initerr(err_ret, filename) < 0)
return NULL;
if (PySys_Audit("compile", "OO", Py_None, err_ret->filename) < 0) {
return NULL;
}
if ((tok = PyTokenizer_FromFile(fp, enc, ps1, ps2)) == NULL) {
err_ret->error = E_NOMEM;
return NULL;
}
if (*flags & PyPARSE_TYPE_COMMENTS) {
tok->type_comments = 1;
}
Py_INCREF(err_ret->filename);
tok->filename = err_ret->filename;
return parsetok(tok, g, start, err_ret, flags);
}(1) 파서-토크나이저는 실행 전에 토크나이저에서 사용하는 모든 상태를 저장하는 임시 데이터 구조인 tok_state를 초기화
- tok_state 구조체
/* Tokenizer state */
struct tok_state {
/* Input state; buf <= cur <= inp <= end */
/* NB an entire line is held in the buffer */
char *buf; /* Input buffer, or NULL; malloc'ed if fp != NULL */
char *cur; /* Next character in buffer */
char *inp; /* End of data in buffer */
const char *end; /* End of input buffer if buf != NULL */
const char *start; /* Start of current token if not NULL */
int done; /* E_OK normally, E_EOF at EOF, otherwise error code */
/* NB If done != E_OK, cur must be == inp!!! */
FILE *fp; /* Rest of input; NULL if tokenizing a string */
int tabsize; /* Tab spacing */
int indent; /* Current indentation index */
int indstack[MAXINDENT]; /* Stack of indents */
int atbol; /* Nonzero if at begin of new line */
int pendin; /* Pending indents (if > 0) or dedents (if < 0) */
const char *prompt, *nextprompt; /* For interactive prompting */
int lineno; /* Current line number */
int first_lineno; /* First line of a single line or multi line string
expression (cf. issue 16806) */
int level; /* () [] {} Parentheses nesting level */
/* Used to allow free continuations inside them */
char parenstack[MAXLEVEL];
int parenlinenostack[MAXLEVEL];
PyObject *filename;
/* Stuff for checking on different tab sizes */
int altindstack[MAXINDENT]; /* Stack of alternate indents */
/* Stuff for PEP 0263 */
enum decoding_state decoding_state;
int decoding_erred; /* whether erred in decoding */
int read_coding_spec; /* whether 'coding:...' has been read */
char *encoding; /* Source encoding. */
int cont_line; /* whether we are in a continuation line. */
const char* line_start; /* pointer to start of current line */
const char* multi_line_start; /* pointer to start of first line of
a single line or multi line string
expression (cf. issue 16806) */
PyObject *decoding_readline; /* open(...).readline */
PyObject *decoding_buffer;
const char* enc; /* Encoding for the current str. */
char* str;
char* input; /* Tokenizer's newline translated copy of the string. */
int type_comments; /* Whether to look for type comments */
/* async/await related fields (still needed depending on feature_version) */
int async_hacks; /* =1 if async/await aren't always keywords */
int async_def; /* =1 if tokens are inside an 'async def' body. */
int async_def_indent; /* Indentation level of the outermost 'async def'. */
int async_def_nl; /* =1 if the outermost 'async def' had at least one
NEWLINE token after it. */
};(2) 토크나이저 상태는 커서의 현재 위치 같은 정보를 저장 (Parser/tokenizer.h)
- Parser/tokenizer.h
/* Tokenizer state */
struct tok_state {
/* Input state; buf <= cur <= inp <= end */
/* NB an entire line is held in the buffer */
char *buf; /* Input buffer, or NULL; malloc'ed if fp != NULL */
char *cur; /* Next character in buffer */
char *inp; /* End of data in buffer */
const char *end; /* End of input buffer if buf != NULL */
const char *start; /* Start of current token if not NULL */
int done; /* E_OK normally, E_EOF at EOF, otherwise error code */
/* NB If done != E_OK, cur must be == inp!!! */
FILE *fp; /* Rest of input; NULL if tokenizing a string */
int tabsize; /* Tab spacing */
int indent; /* Current indentation index */
int indstack[MAXINDENT]; /* Stack of indents */
int atbol; /* Nonzero if at begin of new line */
int pendin; /* Pending indents (if > 0) or dedents (if < 0) */
const char *prompt, *nextprompt; /* For interactive prompting */
int lineno; /* Current line number */
int first_lineno; /* First line of a single line or multi line string
expression (cf. issue 16806) */
int level; /* () [] {} Parentheses nesting level */
/* Used to allow free continuations inside them */
char parenstack[MAXLEVEL];
int parenlinenostack[MAXLEVEL];
PyObject *filename;
/* Stuff for checking on different tab sizes */
int altindstack[MAXINDENT]; /* Stack of alternate indents */
/* Stuff for PEP 0263 */
enum decoding_state decoding_state;
int decoding_erred; /* whether erred in decoding */
int read_coding_spec; /* whether 'coding:...' has been read */
char *encoding; /* Source encoding. */
int cont_line; /* whether we are in a continuation line. */
const char* line_start; /* pointer to start of current line */
const char* multi_line_start; /* pointer to start of first line of
a single line or multi line string
expression (cf. issue 16806) */
PyObject *decoding_readline; /* open(...).readline */
PyObject *decoding_buffer;
const char* enc; /* Encoding for the current str. */
char* str;
char* input; /* Tokenizer's newline translated copy of the string. */
int type_comments; /* Whether to look for type comments */
/* async/await related fields (still needed depending on feature_version) */
int async_hacks; /* =1 if async/await aren't always keywords */
int async_def; /* =1 if tokens are inside an 'async def' body. */
int async_def_indent; /* Indentation level of the outermost 'async def'. */
int async_def_nl; /* =1 if the outermost 'async def' had at least one
NEWLINE token after it. */
};- 파서-토크나이저는 tok_get()으로 다음 토큰을 얻고 그 아이디를 파서로 전달
// Parser/tokenizer.c L1174
/* Get next token, after space stripping etc. */
static int
tok_get(struct tok_state *tok, const char **p_start, const char **p_end)
{
int c;
int blankline, nonascii;
*p_start = *p_end = NULL;
nextline:
tok->start = NULL;
blankline = 0;
/* Get indentation level */
if (tok->atbol) {
...
return PyToken_OneChar(c);
}- 파서는 파서 생성기 오토마타(DFA)로 CST에 노드를 추가
640줄이 넘는 tok_get()은 CPython 코드 중에서도 손꼽히게 복잡한 부분중 하나. 루프에서 토크나이저와 파서를 호출하는 과정은 아래와 같음
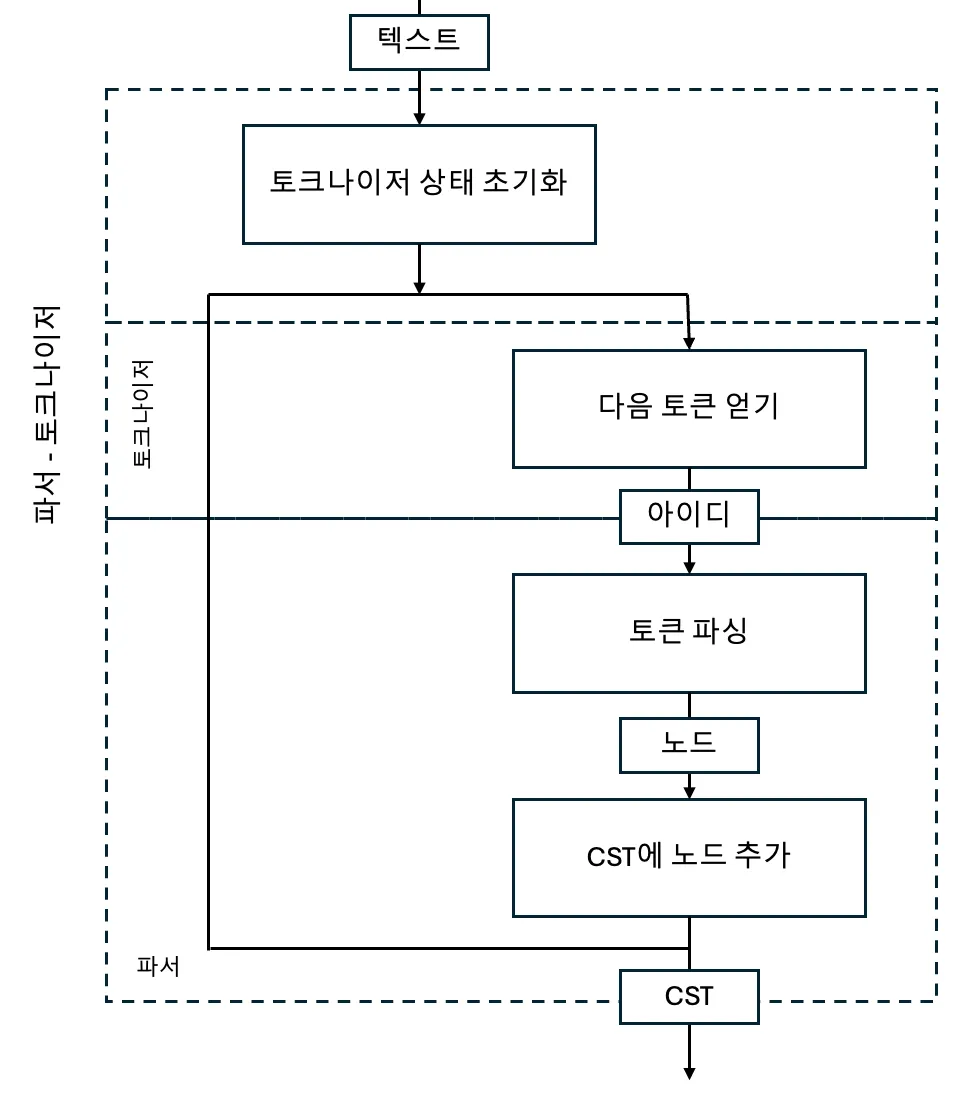
- CST→AST로 변환하려면 PyParser_ParseFileObject()에서 반환된 CST의 루트인 node가 필요
node *
PyParser_ParseFileObject(FILE *fp, PyObject *filename,
const char *enc, grammar *g, int start,
const char *ps1, const char *ps2,
perrdetail *err_ret, int *flags)
{
struct tok_state *tok;
if (initerr(err_ret, filename) < 0)
return NULL;
if (PySys_Audit("compile", "OO", Py_None, err_ret->filename) < 0) {
return NULL;
}
if ((tok = PyTokenizer_FromFile(fp, enc, ps1, ps2)) == NULL) {
err_ret->error = E_NOMEM;
return NULL;
}
if (*flags & PyPARSE_TYPE_COMMENTS) {
tok->type_comments = 1;
}
Py_INCREF(err_ret->filename);
tok->filename = err_ret->filename;
return parsetok(tok, g, start, err_ret, flags);
}
노드 구조체는 Include/node.h에서 정의
typedef struct _node {
short n_type;
char *n_str;
int n_lineno;
int n_col_offset;
int n_nchildren;
struct _node *n_child;
int n_end_lineno;
int n_end_col_offset;
} node;
CST는 구문, 토큰 아이디, 심벌을 모두 포함하기 때문에 컴파일러가 사용하기에는 적합하지 않음
AST를 살펴보기에 앞서 파서 단계의 결과를 확인하는 방법이 있는데, parser 모듈은 C함수의 파이썬 API를 제공
>>> import parser
st<stdin>:1: DeprecationWarning: The parser module is deprecated and will be removed in future versions of Python
>>> st = parser.expr('a+1')
>>>
>>>
>>> pprint(parser.st2list(st))
[258,
[332,
[306,
[310,
[311,
[312,
[313,
[316,
[317,
[318,
[319,
[320,
[321, [322, [323, [324, [325, [1, 'a']]]]]],
[14, '+'],
[321, [322, [323, [324, [325, [2, '1']]]]]]]]]]]]]]]]],
[4, ''],
[0, '']]- Parser 모듈의 출력은 숫자형식으로 make regen-grammar 단계에서 Include/token.h파일에 저장된 코튼과 심벌의 번호와 같음
좀더 보기 쉽게 symbol과 token 모듈의 모든 번호로 딕셔너리를 만든 후 parser.st2list()의 출력을 토큰과 심벌의 이름으로 재귀적으로 바꾸면 아래와 같음
import symbol
import token
import parser
from pprint import pprint
def lex(expression):
symbols = {v: k for k, v in symbol.__dict__.items() if isinstance(v, int)}
tokens = {v: k for k, v in token.__dict__.items() if isinstance(v, int)}
lexicon = {**symbols, **tokens}
st = parser.expr(expression)
st_list = parser.st2list(st)
def replace(l: list):
r = []
for i in l:
if isinstance(i, list):
r.append(replace(i))
else:
if i in lexicon:
r.append(lexicon[i])
else:
r.append(i)
return r
return replace(st_list)
pprint(lex("a + 1"))['eval_input',
['testlist',
['test',
['or_test',
['and_test',
['not_test',
['comparison',
['expr',
['xor_expr',
['and_expr',
['shift_expr',
['arith_expr',
['term',
['factor', ['power', ['atom_expr', ['atom', ['NAME', 'a']]]]]],
['PLUS', '+'],
['term',
['factor',
['power', ['atom_expr', ['atom', ['NUMBER', '1']]]]]]]]]]]]]]]]],
['NEWLINE', ''],
['ENDMARKER', '']]
- symbol은 arith_expr 처럼 소문자로, 토큰은 NUMBER처럼 대문자로 출력
6.3 추상 구문 트리
- 파서가 생성한 CST를 실행가능하면서 좀 더 논리적으로 변환하는 단계
- CST는 코드 파일의 텍스트를 있는 그대로 표현하는 구조로, 텍스트로부터 토큰을 추출하여 토큰 종류만 구분해 둔 상태에 불과
- CST로 기본적인 문법 구조는 알 수 있지만 함수, 스코프, 루프 같은 파이썬 언어 사양에 대한 의미를 결정할 수 없음
- 코드를 컴파일 하기 전 CST를 실제 파이썬 언어구조와 의미 요소를 표현하는 고수준 구조인 AST로 변환해야 함
- 예를 들어 AST에서 이항 연산은 표현식의 한 종류인 BinOp로 표현. 해당 표현식은 세가지 요소로 이루어짐
- left: 왼쪽 항
- op: 연산자(+, -, * 등)
- right: 오른쪽 항
다음은 a + 1 에 대한 AST
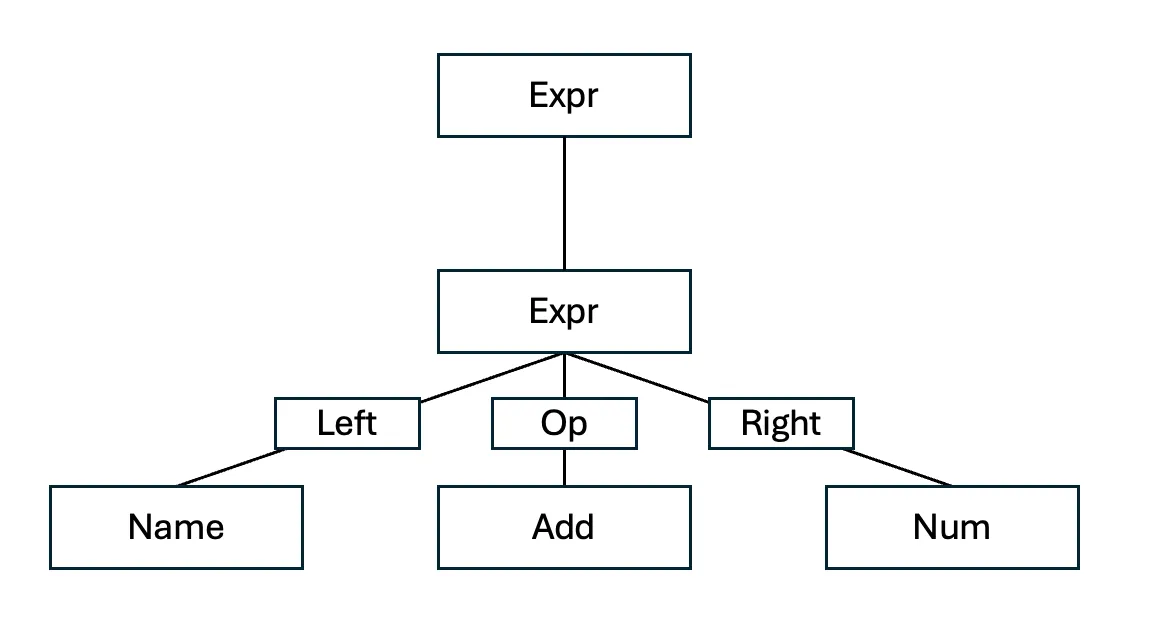
- AST는 CPython 파싱 과정 중에 생성하지만 표준 라이브러리 ast모듈을 사용해서 파이썬 코드에서 AST를 생성할 수도 있음
6.3.1 AST 연관된 소스 파일 목록
- Include/python-ast.h: Parser/asdl_c.py 로 생성한 AST 노드 타입 선언
- parser/Python.asdl: 도메인 특화 언어인 ASDL(abstract syntax description language) 5로 작성된 ast 노드 타입들과 프로퍼티 목록
- Python/ast.c: AST 구현
6.3.2 인스타비즈로 AST 시각화하기
$ pip install instaviz
- AST와 컴파일된 코드를 웹 인터페이스로 시각화 하는 파이썬 패키지
❯ python
Python 3.9.20 (main, Sep 6 2024, 19:03:56)
[Clang 15.0.0 (clang-1500.3.9.4)] on darwin
Type "help", "copyright", "credits" or "license" for more information.
>>> import instaviz
>>> def example():
... a = 1
... b = a + 1
... return b
...
>>>
>>> instaviz.show(example)
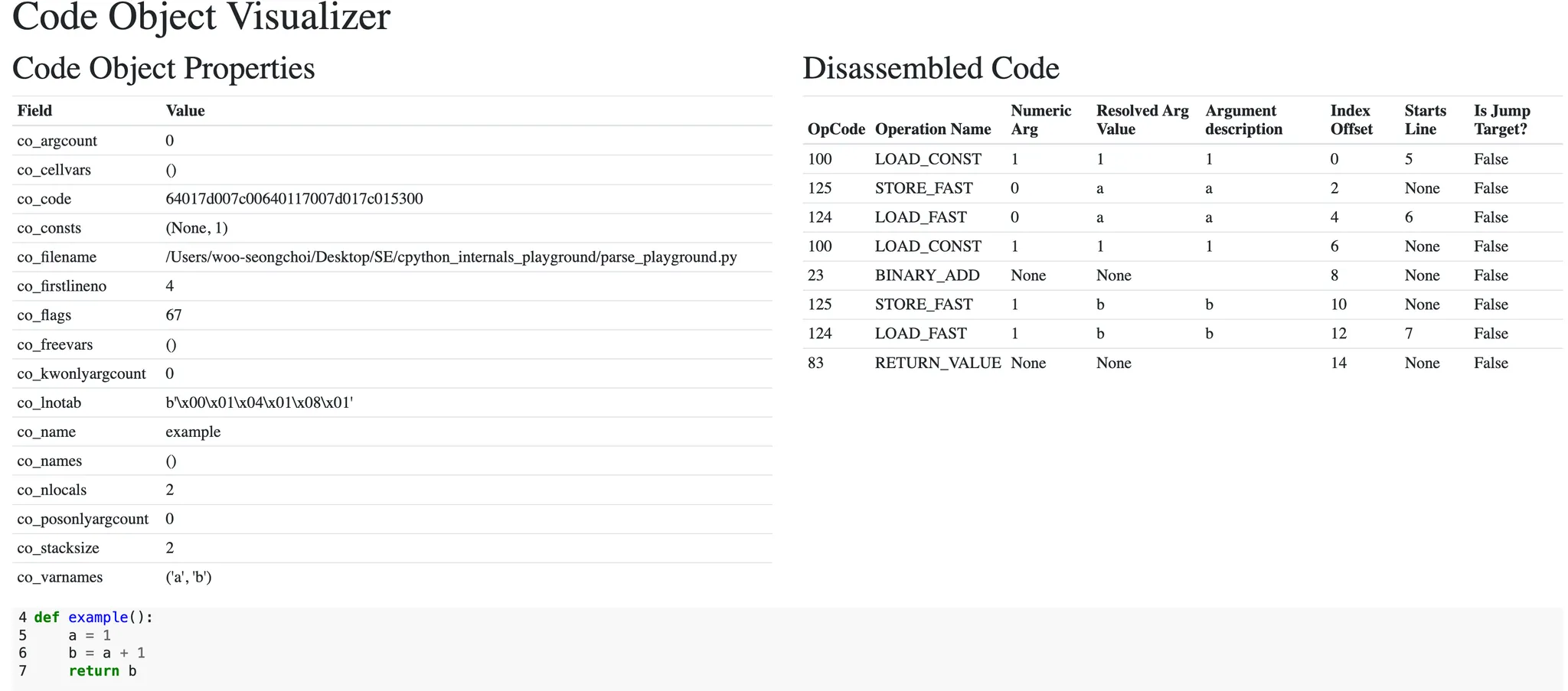
- 트리의 각 노드의 타입은 AST 노드 클래스
- ast 모듈에서 찾을 수 있는 노드 클래스들은 모두 _ast.AST를 상속
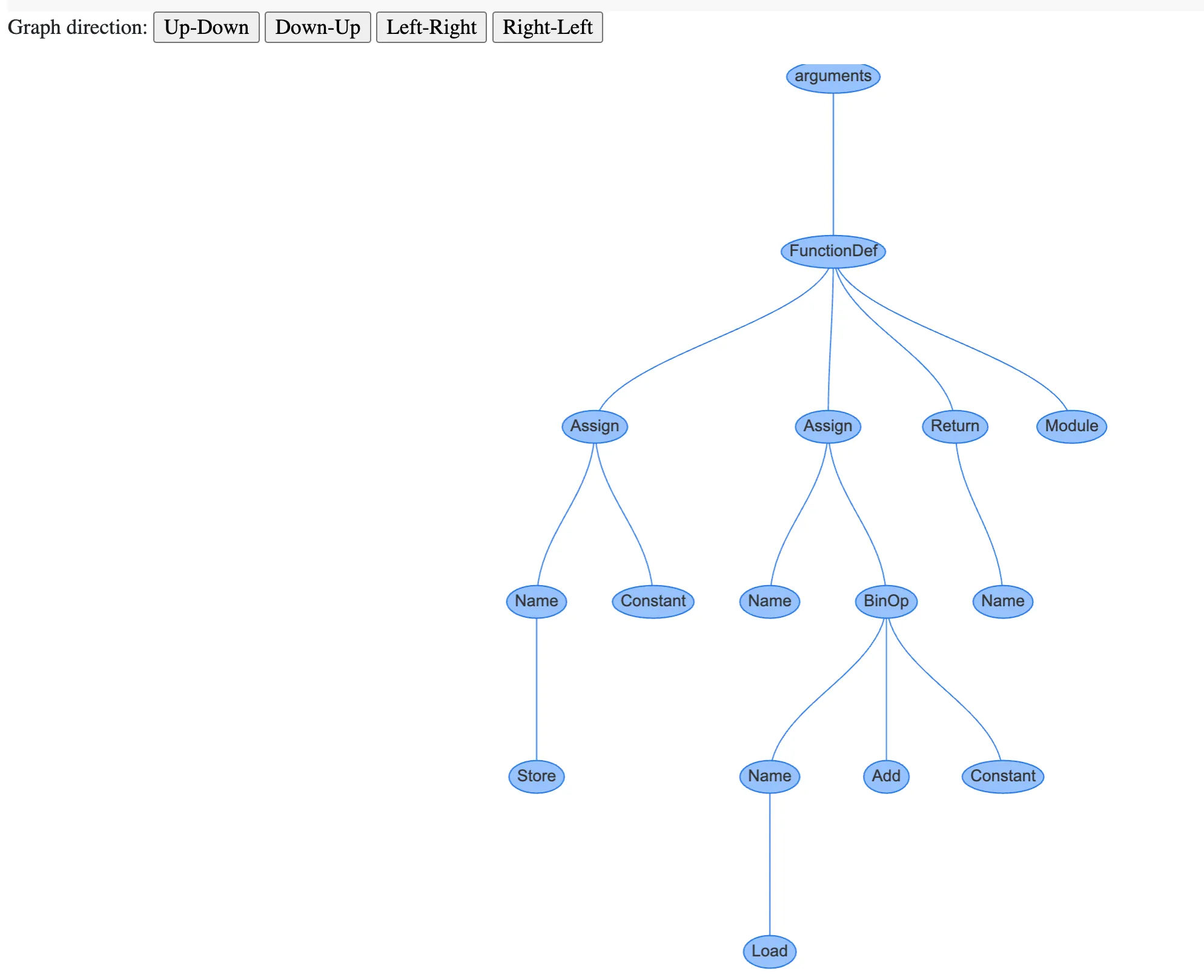
- CST와 달리, AST의 노드들은 특정 프로퍼티들을 통해 자식 노드와 연결됨
- b = a + 1 이 선언된 줄과 연결된 assign 노드를 클릭하면 아래와 같음
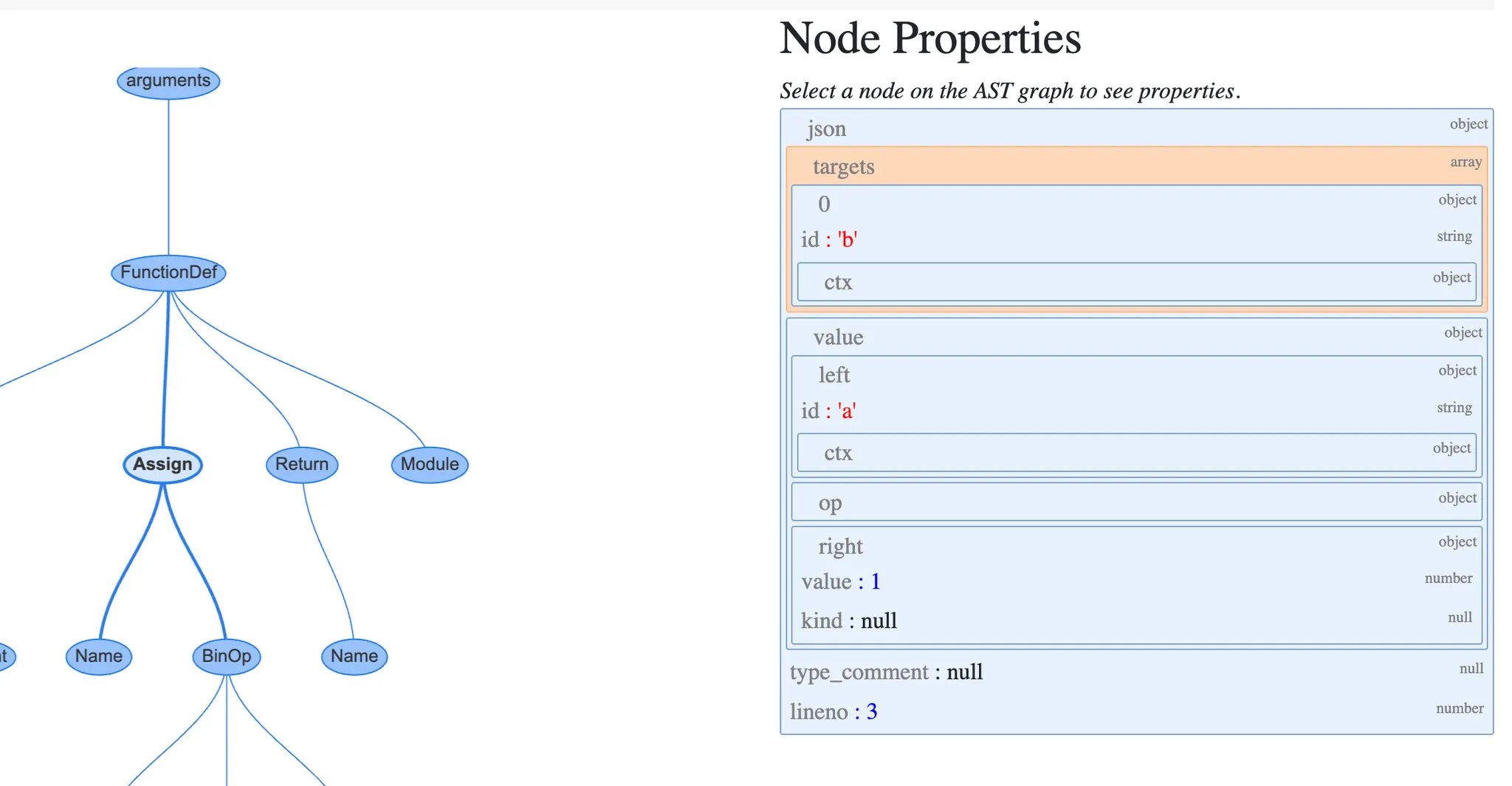
- Assign 노드는 2개의 프로퍼티를 가짐
- targets는 값이 할당될 이름의 목록. 언패킹을 통해 한 번에 여러 이름에 값을 할당할 수 있기 때문에 목록이 필요
- value는 이름에 할당할 값. 이 경우에 BinOp 표현식 a + 1 이 할당됨
- BinOp노드는 세 개의 프로퍼티를 가짐
- left: 왼쪽 항
- op: 연산자, 이 경우에는 더 하기를 뜻하는 Add 노드(+)
- right: 오른쪽 항
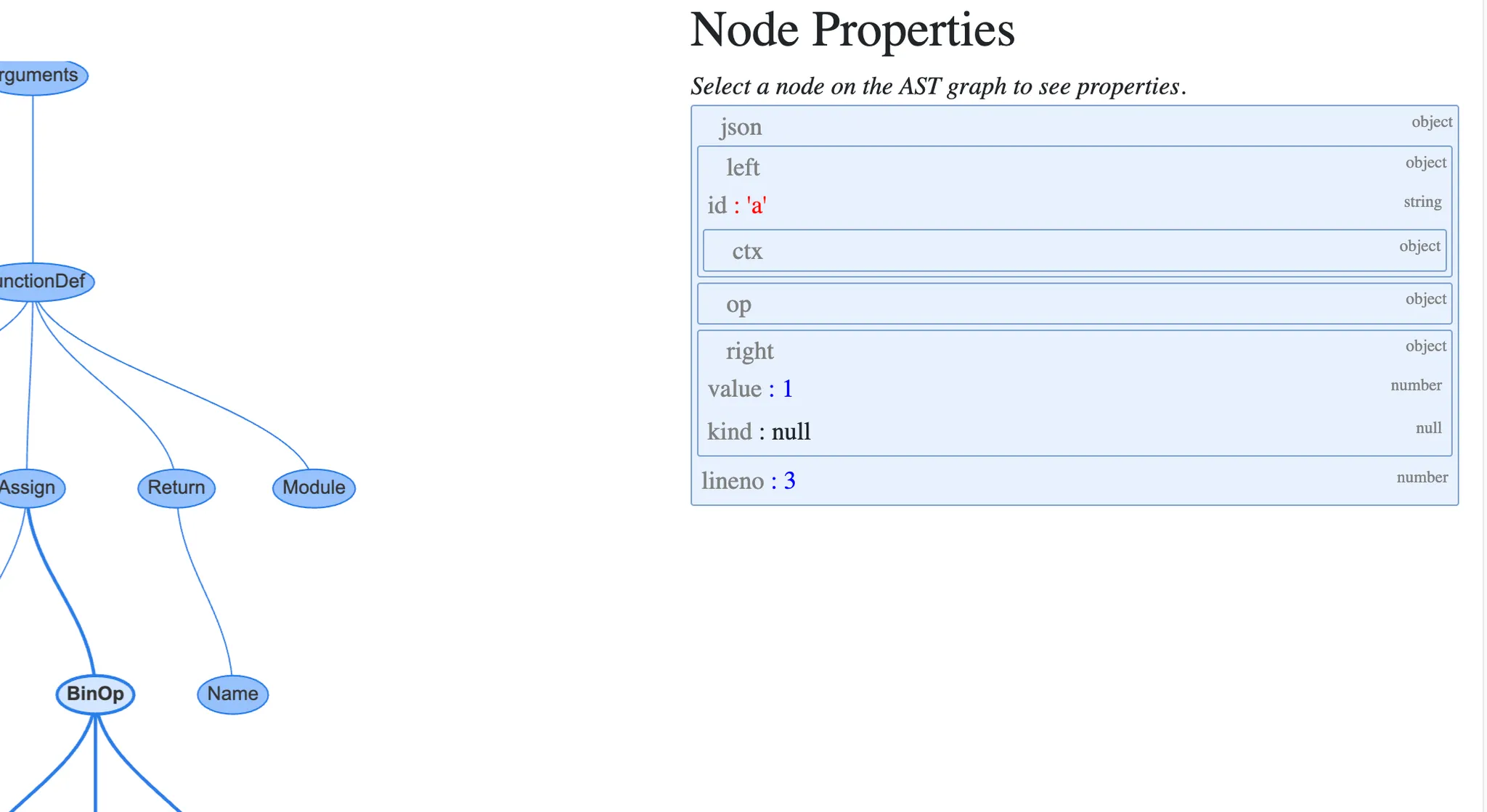
6.3.3 AST 컴파일
- C에서 AST를 컴파일하는 것을 매우 복잡한 작업으로 Python/ast.c 모듈은 5000줄이 넘는 코드로 이루어져 있음
- AST의 공개 API는 CST와 파일 이름, 컴파일러 플래그 ,메모리 저장 영역을 인자로 받음
- 반환 타입은 파이썬 모듈을 표현하는 mod_ty 타입으로 Include/Python-ast.h 에서 정의
mod_ty는 아래 4가지 모듈 타입 중 하나를 담는 컨테이너 구조체
- Module
- Interactive
- Expression
- FunctionType
- 모듈 타입은 Parser/Python.asdl에서 정의하는데 문장, 표현식, 연산자, 컴프리헨션 타입들도 찾을 수 있음
- AST가 생성하는 클래스들과 표준 라이브러리 ast 모듈의 클래스들은 Parser/Python.asdl에서 정의하는 타입들
Parser/Python.asdl 파일 내용의 일부
-- ASDL's 4 builtin types are:
-- identifier, int, string, constant
module Python
{
mod = Module(stmt* body, type_ignore* type_ignores)
| Interactive(stmt* body)
| Expression(expr body)
| FunctionType(expr* argtypes, expr returns)
- ast 모듈은 문법을 다시 생성할 때 Include/Python-ast.h를 임포트하는데 이 파일은 Parser/Python.asdl에서 자동으로 생성됨
- Include/Python-ast.h 파라미터와 이름은 Parser/Python.asdl의 정의를 따름
- Include/Python-ast.h 의 mod_ty 타입은 Parser/Python.asdl 의 Module 정의로부터 생성됨
// Include/Python-ast.h
struct _mod {
enum _mod_kind kind;
union {
struct {
asdl_seq *body;
asdl_seq *type_ignores;
} Module;
struct {
asdl_seq *body;
} Interactive;
struct {
expr_ty body;
} Expression;
struct {
asdl_seq *argtypes;
expr_ty returns;
} FunctionType;
} v;
};
- Python/ast.c 는 이 C 헤더 파일에서 제공하는 구조체들을 사용해 필요한 데이터를 가리키는 포인터를 담은 구조체들을 신속하게 생성
- AST의 진입점인 PyAST_FromNodeObject()는 TYPE(n)에 대한 switch 문을 실행
- TYPE()은 CST 노드의 타입을 결정하는 매크로로 결과로 심벌 또는 토큰 타입을 반환
- 루트 노드의 타입은 항상 Module, Interactive, Expression, FunctionType 중 하나
- file_input일 경우 Module 타입
- REPL 등으로 들어오는 eval_input 인 경우는 Expression 타입
- Python/ast.c에는 각 타입에 대응되는 ast_for_xxx 이름의 C 함수들이 구현되어있음
- 이 함수들은 CST의 노드 중에 해당 문에 대한 프로퍼티를 찾음
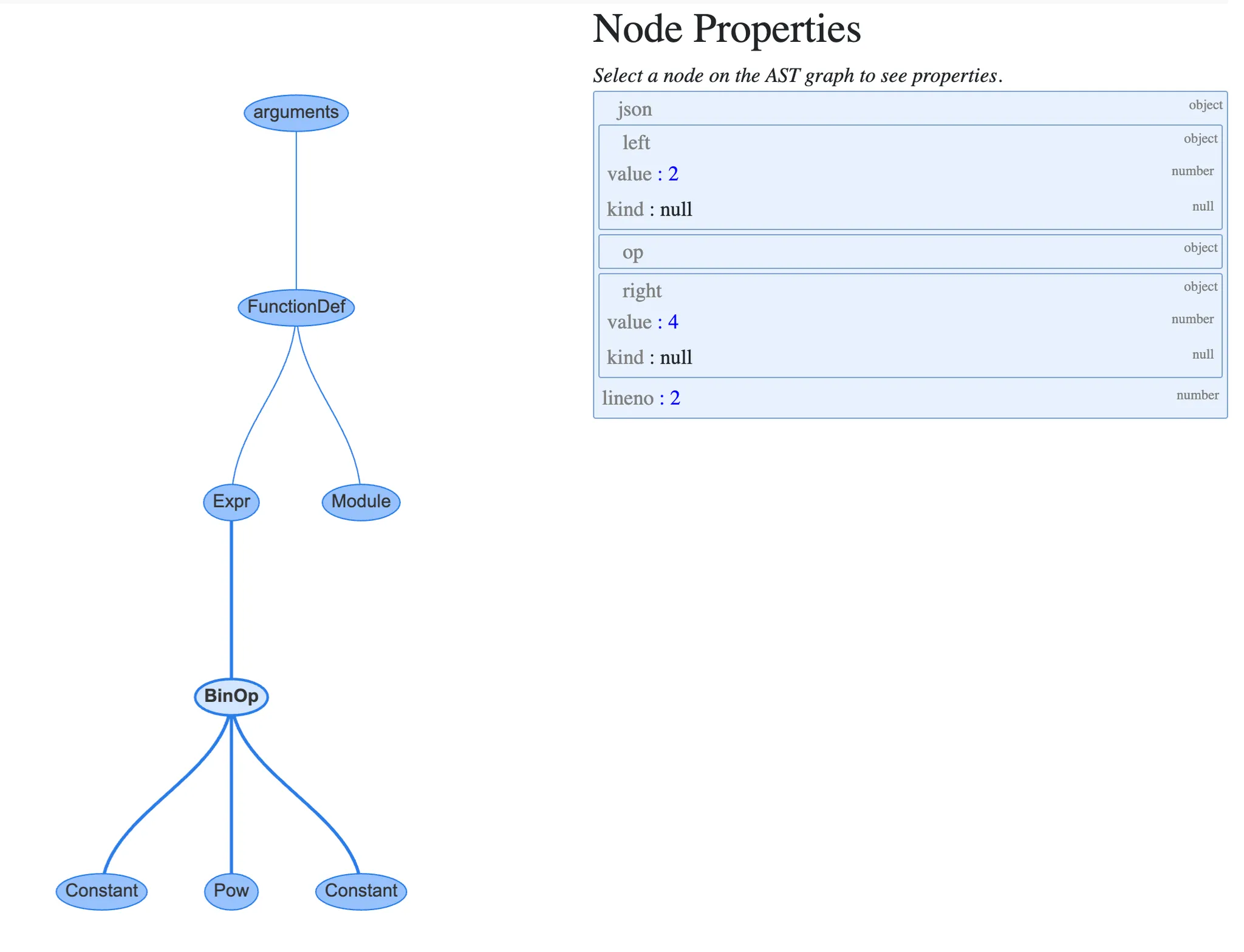
ex) 2 의 4제곱을 뜻하는 2 ** 4같은 제곱에 대한 표현식
- ast_for_power()는 연산자가 Pow(제곱), 좌측은 e(2), 우측은 f(4)인 BinOp를 반환
// Python/ast.c L2716
static expr_ty
ast_for_power(struct compiling *c, const node *n)
{
/* power: atom trailer* ('**' factor)*
*/
expr_ty e;
REQ(n, power);
e = ast_for_atom_expr(c, CHILD(n, 0));
if (!e)
return NULL;
if (NCH(n) == 1)
return e;
if (TYPE(CHILD(n, NCH(n) - 1)) == factor) {
expr_ty f = ast_for_expr(c, CHILD(n, NCH(n) - 1));
if (!f)
return NULL;
e = BinOp(e, Pow, f, LINENO(n), n->n_col_offset,
n->n_end_lineno, n->n_end_col_offset, c->c_arena);
}
return e;
}
import instaviz
def foo():
2**4
instaviz.show(foo)
요약
- 모든 타입의 문과 표현식에는 ast_for_xx() 생성자 함수가 있음
- 함수의 인자들은 Parser/Python.asdl에서 정의하며 표준 라이브러리의 ast 모듈을 통해 외부에 제공
- 표현식 또는 문이 자식 노드를 가지고 있으면 깊이 우선 탐색을 통해 자식 노드에 대한 ast_for_xx () 함수를 먼저 호출
6.4 중요한 용어들
- AST(Abstract Syntax Tree): 파이썬 문법과 문장들에 대한 문맥 있는 트리 표현
- CST(Concrete Syntax Tree): 토큰과 심벌에 대한 문맥 없는 트리 표현
- 파스 트리 (Parse Tree): CST의 다른 이름
- 토큰: 심벌의 종류 중 하나(ex) +)
- 토큰화: 텍스트를 토큰으로 변환하는 과정
- 파싱: 텍스트를 CST나 AST로 변환하는 과정
6.5 예제: ‘거의 같음’ 비교 연산자 추가하기
- 새로운 문법인 거의 같음 연산자 (’~=’)을 추가하고 CPython을 컴파일
- 아래와 같이 동작
- 정수와 부동 소수점을 비교할 때 부동 소수점은 정수로 변환해 비교
- 정수와 정수를 비교할 때는 일반 동등 연산자를 사용
REPL에서 새 연산자를 사용하면 아래와 같은 결과를 볼 수 있어야 함
>>> 1 ~= 1
True
>>> 1 ~= 1.0
True
>>> 1 ~= 1.01
True
>>> 1 ~= 1.9
False
- 먼저 CPython 문법을 변경해야 함. 비교 연산자들은 Grammar/python.gram 파일에 comp_op 심벌로 정의 (L398: L413)
comparison[expr_ty]:
| a=bitwise_or b=compare_op_bitwise_or_pair+ {
_Py_Compare(a, CHECK(_PyPegen_get_cmpops(p, b)), CHECK(_PyPegen_get_exprs(p, b)), EXTRA) }
| bitwise_or
compare_op_bitwise_or_pair[CmpopExprPair*]:
| eq_bitwise_or
| noteq_bitwise_or
| lte_bitwise_or
| lt_bitwise_or
| gte_bitwise_or
| gt_bitwise_or
| notin_bitwise_or
| in_bitwise_or
| isnot_bitwise_or
| is_bitwise_or
| ale_bitwise_or (추가된 내용)
- compare_op_bitwise_or_pair 식에 ale_bitwise_or를 허용
L414: L424 에서 ale_bitwise_or 추가해서 ‘~=’ 단말 기호를 포함하는 식을 정의
eq_bitwise_or[CmpopExprPair*]: '==' a=bitwise_or { _PyPegen_cmpop_expr_pair(p, Eq, a) }
noteq_bitwise_or[CmpopExprPair*]:
| (tok='!=' { _PyPegen_check_barry_as_flufl(p, tok) ? NULL : tok}) a=bitwise_or {_PyPegen_cmpop_expr_pair(p, NotEq, a) }
lte_bitwise_or[CmpopExprPair*]: '<=' a=bitwise_or { _PyPegen_cmpop_expr_pair(p, LtE, a) }
lt_bitwise_or[CmpopExprPair*]: '<' a=bitwise_or { _PyPegen_cmpop_expr_pair(p, Lt, a) }
gte_bitwise_or[CmpopExprPair*]: '>=' a=bitwise_or { _PyPegen_cmpop_expr_pair(p, GtE, a) }
gt_bitwise_or[CmpopExprPair*]: '>' a=bitwise_or { _PyPegen_cmpop_expr_pair(p, Gt, a) }
notin_bitwise_or[CmpopExprPair*]: 'not' 'in' a=bitwise_or { _PyPegen_cmpop_expr_pair(p, NotIn, a) }
in_bitwise_or[CmpopExprPair*]: 'in' a=bitwise_or { _PyPegen_cmpop_expr_pair(p, In, a) }
isnot_bitwise_or[CmpopExprPair*]: 'is' 'not' a=bitwise_or { _PyPegen_cmpop_expr_pair(p, IsNot, a) }
is_bitwise_or[CmpopExprPair*]: 'is' a=bitwise_or { _PyPegen_cmpop_expr_pair(p, Is, a) }
ale_bitwise_or[CmpopExprPair*]: '~=' a=bitwise_or { _PyPegen_cmpop_expr_pair(p, ALE, a) } (추가된 내용)
- _PyPegen_cmpop_expr_pair(p, ALE, a) 함수 호출은 AST에서 ‘거의 같음’ 연산자를 뜻하는 AlE(Almost Equal) 타입 cmpop 노드를 가져옴
- Grammar/Tokens에 토큰 추가 (L54)
ELLIPSIS '...'
COLONEQUAL ':='
ALMOSTEQUAL '~=' (추가된 내용)
- 변경된 문법과 토큰을 C코드에 반영하기 위해 헤더를 다시 생성
❯ make regen-token regen-pegen
# Regenerate Doc/library/token-list.inc from Grammar/Tokens
# using Tools/scripts/generate_token.py
python3.9 ./Tools/scripts/generate_token.py rst \\
./Grammar/Tokens \\
./Doc/library/token-list.inc
# Regenerate Include/token.h from Grammar/Tokens
# using Tools/scripts/generate_token.py
python3.9 ./Tools/scripts/generate_token.py h \\
./Grammar/Tokens \\
./Include/token.h
# Regenerate Parser/token.c from Grammar/Tokens
# using Tools/scripts/generate_token.py
python3.9 ./Tools/scripts/generate_token.py c \\
./Grammar/Tokens \\
./Parser/token.c
# Regenerate Lib/token.py from Grammar/Tokens
# using Tools/scripts/generate_token.py
python3.9 ./Tools/scripts/generate_token.py py \\
./Grammar/Tokens \\
./Lib/token.py
PYTHONPATH=./Tools/peg_generator python3.9 -m pegen -q c \\
./Grammar/python.gram \\
./Grammar/Tokens \\
-o ./Parser/pegen/parse.new.c
python3.9 ./Tools/scripts/update_file.py ./Parser/pegen/parse.c ./Parser/pegen/parse.new.c
- 헤더를 다시 생성하면 토크나이저도 자동으로 변경됨. Parser/token.c 파일 안에 _PyParser_TokenNames 배열에 "ALMOSTEQUAL"추가 및 PyToken_TwoChars()함수의 case에 ‘~’와 ‘=’가 추가된 것을 확인 할 수 있음
const char * const _PyParser_TokenNames[] = {
...
"ALMOSTEQUAL",
...
};
int
PyToken_TwoChars(int c1, int c2)
{
switch (c1){
case '~':
switch (c2) {
case '=': return ALMOSTEQUAL;
}
break;
...
- CPython을 다시 컴파일하고 REPL을 실행해보면 토크나이저는 새 토큰을 처리할 수 있지만 AST는 처리하지 못함
ast.c의 ast_for_comp_op()는 ALMOSTEQUAL을 올바른 비료 연산자로 인식할 수 없기 때문에 예외를 발생시킴
Parser/Python.asdl에 정의하는 Compare 표현식은 좌측 표현식 left, 연산자목록인 ops, 비교할 표현식 목록인 comparators로 이루어져 있음
Compare 정의는 cmpop 열거 형을 참조하면되고, 이 열거형은 비교 연산자로 사용할 수 있는 AST 리프 노드의 목록. 여기에 ‘거의 같음’ 연산자인 AlE를 추가
cmpop = Eq | NotEq | Lt | LtE | Gt | GtE | Is | IsNot | In | NotIn | AlE
$ make regen-ast
Incude/Python-ast.h에서 비교 연산자를 정의하는 열거형인 _cmpop에 AlE가 추가된 것을 확인할 수 있음
//Include/Python-ast.h L30
typedef enum _cmpop { Eq=1, NotEq=2, Lt=3, LtE=4, Gt=5, GtE=6, Is=7, IsNot=8,
In=9, NotIn=10, AlE=11 } cmpop_ty;
AST는 ALMOSTEQUAL 토큰이 비교 연산자인 AlE라는 것을 아직 알 수 없어서, 토큰을 연산자로 인식할 수 있게 AST관련 C 코드를 수정
Python/ast.c의 ast_for_comp_op()로 이동해서 switch문을 찾아보면, _cmpop 열거형 값 중 하나를 반환 함
static cmpop_ty
ast_for_comp_op(struct compiling *c, const node *n)
{
/* comp_op: '<'|'>'|'=='|'>='|'<='|'!='|'in'|'not' 'in'|'is'
|'is' 'not'
*/
REQ(n, comp_op);
if (NCH(n) == 1)
{
n = CHILD(n, 0);
switch (TYPE(n))
{
case LESS:
return Lt;
case GREATER:
return Gt;
case ALMOSTEQUAL: // 추가된 내용
return AlE; // 추가된 내용
case EQEQUAL: /* == */
return Eq;
case LESSEQUAL:
return LtE;
case GREATEREQUAL:
return GtE;
case NOTEQUAL:
return NotEq;
case NAME:
if (strcmp(STR(n), "in") == 0)
return In;
if (strcmp(STR(n), "is") == 0)
return Is;
/* fall through */
이제 토크나이저와 AST모두 코드를 파싱할 수 있지만 컴파일러는 아직 이 연산자를 실행하는 방법을 모름
AST로 거의 같음 연산자를 아래와 같이 확인해볼 수 있음
import ast
m = ast.parse('1 ~= 2')
m.body[0].value.ops[0]
<_ast.AlE object at 0x111111>
'Python' 카테고리의 다른 글
| [책리뷰] 파이썬 클린 코드 Chapter 3. 좋은 코드의 일반적인 특징 (0) | 2024.11.10 |
|---|---|
| [책리뷰] CPython 파헤치기 5장. 구성과 입력 (0) | 2024.11.10 |
| [책리뷰] CPython 파헤치기 4장. 파이썬 언어와 문법 (0) | 2024.11.10 |
| pathlib 모듈 (0) | 2024.10.20 |
| [책리뷰] 파이썬 클린 코드 Chapter 2. Pythonic 코드 (2) (0) | 2024.09.29 |