뒤돌아보기

함수의 재귀적 호출의 의해

재귀함수의 기본적인 이해

void Recursive(void)
{
	cout<<"Recursive call!"<<endl;
	Recursive(); **//함수 나 자신을 재호출** 
}

• 완료되지 않은 함수를 다시 호출하는 것 가능? → 가능
• Recursive 함수가 호출되면, 원본으로부터 함수의 복사본이 만들어져서 복사본이 실행되는 구조로 이해

Recursive function은 한번 호출되면 계속 호출되는 문제때문에 탈출조건이 필요

재귀함수의 디자인 사례

재귀함수는 자료구조나 알고리즘의 어려운 문제를 단순화하는데 사용되는 중요한 무기

→ 재귀적인 수학 수식을 코드로 그대로 옮길 수 있음

ex) factorial

$$ f(n)= \begin{cases} n \times f(n-1), &n \ge 1 \\ 1, &n=0 \end{cases}
$$

#include <iostream>
using namespace std;

int factorial(int n)
{
	if (n == 0)
		return 1;
	else
		return n * factorial(n - 1);
}

int main()
{
	cout << "1! = " << factorial(1) << endl;
	cout << "2! = " << factorial(2) << endl;
	cout << "3! = " << factorial(3) << endl;
	cout << "4! = " << factorial(4) << endl;
	cout << "9! = " << factorial(9) << endl;
	return 0;
}

재귀의 활용

피보나치 수열: Fibonacci Sequence

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ...

#include <iostream>
using namespace std;

int fibo(int num)
{
	cout << "function call param " << num << endl;
	if (num == 1)
		return 0;
	else if (num == 2)
		return 1;
	else
		return fibo(num - 1) + fibo(num - 2);
}

int main()
{
	fibo(7);
	return 0;
}

function call param 7
function call param 6
function call param 5
function call param 4
function call param 3
function call param 2
function call param 1
function call param 2
function call param 3
function call param 2
function call param 1
function call param 4
function call param 3
function call param 2
function call param 1
function call param 2
function call param 5
function call param 4
function call param 3
function call param 2
function call param 1
function call param 2
function call param 3
function call param 2
function call param 1

return fibo(n-1)+fibo(n-2);

• 2개의 fibo 함수가 다시 호출되는데, + 연산자의 왼편에 있는 fibo 함수호출이 완료되어야 비로소 + 연산자의 오른편에 있는 fibo 함수호출이 진행이 된다.

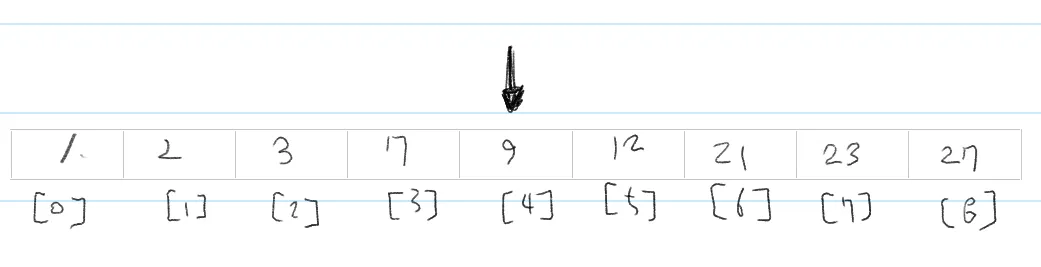
이진 탐색 알고리즘의 재귀적 구현

Binary search 알고리즘도 패턴이 반복됨을 이용해서 recursive function 형태로 만들 수 있음

패턴

• 탐색 범위의 중앙에 목표 값이 저장되었는지 확인
• 저장되지 않았다면 탐색 범위를 반으로 줄여서 다시 탐색 시작

탈출조건

• 탐색 범위의 시작을 의미하는 first가 탐색 범위의 끝을 의미하는 last보다 커지는 경우

함수

int BSearchRecur(int ar[], int first, int last, int target)

위의 패턴과 탈출조건, 그리고 함수 호출 형태만을 이용해 code 작성할 수 있어야 함

#include <iostream>
using namespace std;

int BSearchRecur(int arr[], int first, int last, int target)
{
	if (first > last)
		return -1; // 탐색의 실패를 의미

	int mid = (first + last) / 2;
	if (arr[mid] == target)
		return mid;
	else
	{
		if (arr[mid] > target)
			return BSearchRecur(arr, first, mid - 1, target);
		else
			return BSearchRecur(arr, mid + 1, last, target);
	}
}

int main()
{
	int arr[] = { 1, 3, 5, 7, 9};
	int idx;

	idx = BSearchRecur(arr, 0, sizeof(arr) / sizeof(int) - 1, 7);

	if (idx == -1)
		cout << "탐색 실패" << endl;
	else
		cout << "타겟 저장 인덱스 : " << idx << endl;

	idx = BSearchRecur(arr, 0, sizeof(arr) / sizeof(int) - 1, 4);
	if (idx == -1)
		cout << "탐색 실패" << endl;
	else
		cout << "타겟 저장 인덱스 : " << idx << endl;

	return 0;
}

타겟 저장 인덱스 : 3 탐색 실패

Q. Binary search 알고리즘을 재귀함수 기반으로 구현하는 이유는? 성능도 떨어지는데?

→ 재귀함수에 익숙해지는게 목적

하노이 타워: The Tower of Hanoi

하노이 문제

• 그림을 그려서 step by step 으로 이해
• 코드를 재귀적으로 구성
• 아래 코드와 비교

#include <iostream>
using namespace std;

void HanoiTowerMove(int num, char from, char by, char to)
{
	if (num == 1) //이동할 원반의 수가 1개라면
	{
		cout << "원반 1을 " << from << "에서 " << to << "로 이동" << endl;
	}
	else
	{
		HanoiTowerMove(num - 1, from, to, by);
		cout << "원반 " << num << "을(를) " << from << "에서 " << to << "로 이동" << endl;
		HanoiTowerMove(num - 1, by, from, to);
	}
}

int main()
{
	//막대 A의 원반 3개를 막대 B를 경유하여 막대C로 옮기기
	HanoiTowerMove(3, 'A', 'B', 'C');
	
	return 0;
}

원반 1을 A에서 C로 이동 원반 2을(를) A에서 B로 이동 원반 1을 C에서 B로 이동 원반 3을(를) A에서 C로 이동 원반 1을 B에서 A로 이동 원반 2을(를) B에서 C로 이동 원반 1을 A에서 C로 이동

01-1 자료구조와 알고리즘

"프로그램이란 데이터를 표현하고, 그렇게 표현된 데이터를 처리하는 것이다"

• 자료구조 : 데이터의 표현 및 저장방법
• 알고리즘 : 표현 및 저장된 데이터를 대상으로 하는 '문제의 해결 방법'

→ 자료구조에 따라서 알고리즘은 달라지고, 알고리즘은 자료구조에 의존적

01-2 알고리즘의 성능분석 방법

시간 복잡도(Time complexity)와 공간 복잡도(Space complexity)

• 잘 동작하는 것에 더하여 좋은 성능을 보장하기 위해 자료구조와 알고리즘을 분석하고 평가할 수 있어야 함 (만능은 존재하지 않음)
• 시간복잡도 : 속도에 해당하는 알고리즘의 수행시간 분석 결과 (cpu에 얼마나 부하를 주는가?)
• 공간복잡도 : 메모리 사용량에 대한 분석 결과

일반적으로 알고리즘을 평가할 때 메모리의 사용량보다 실행속도에 초점을 둠. 공간복잡도는 보조적인 역할

Q. 어떻게 속도를 평가하나?

• 특정 상황에 대해서 속도를 재는 것은 무의미
• $\because$ 처리해야 할 데이터 양의 변화에 따라 속도의 증가 및 감소의 정도가 달라지기 때문
• 위의 이유로 알고리즘의 수행속도를 평가할 때 다음과 같은 방식을 취함
  1. 연산의 횟수를 셈
  2. 처리해야 할 데이터의 수 n에 대한 연산횟수의 함수 T(n)을 구성
• 식을 구성하면 데이터 수의 증가에 따른 연산횟수의 변화 정도를 판단할 수 있고, 다른 알고리즘들의 시간복잡도를 비교할 수 있음

알고리즘은 상황에 맞게 종합적으로 사고하고 판단하여 선택해야 함

• 데이터의 수가 많아짐에 따른 연산횟수의 증가 정도가 중요하므로 알고리즘 A가 B보다 훨씬 좋은 알고리즘. T(n)함수에 대한 패턴이 중요함
• 그렇다고 알고리즘 B가 필요없는게 아님
  • B와 같은 성격의 알고리즘은 A보다 구현이 쉬워 데이터의 수가 많지 않고 성능에 덜 민감한 경우라면 구현의 편의를 위해 B를 선택하기도 함

순차 탐색(Linear Search) 알고리즘과 시간 복잡도 분석의 핵심요소

#include<iostream>
using namespace std;

int LSearch(int ar[], int len, int target) // 순차 탐색 알고리즘 적용된 함수
{
	int i;
	for (i = 0; i < len; i++)
	{
		if (ar[i] == target)
			return i; //찾은 대상의 인덱스 값 반환
	}
	return -1;
}

int main(void)
{
	int arr[] = { 3, 5, 2, 4, 9 };

	int idx;

	idx = LSearch(arr, sizeof(arr) / sizeof(int), 4);
	if (idx == -1)
		cout<<"탐색 실패"<<endl;
	else
		cout<<"타겟 저장 인덱스 : "<<idx<<endl;

	idx = LSearch(arr, sizeof(arr) / sizeof(int), 7);
	if (idx == 01)
		cout<<"탐색 실패"<<endl;
	else
		cout<<"타겟 저장 인덱스 : "<<idx<<endl;
	return 0;
}

타겟 저장 인덱스 : 3
타겟 저장 인덱스 : -1

• 좋은 탐색 알고리즘에서는 비교하는 '==' 연산이 적게 수행되어야 함
  • '<'와 '++'는 '=='연산자가 true를 반환할 때까지 수행이 됨

최악의 경우와 최상의 경우

• 탐색의 대상이 되는 요소의 수(ex) 배열길이)가 n인 경우,
  • 운이 좋아서 찾고자 하는 값이 배열의 맨 앞에 저장된 경우, 연산 횟수 1회 (best case)
  • 운이 없어서 찾고자 하는 값이 배열의 맨 뒤에 저장된 경우, 연산 횟수 n회 (worst case)
• 알고리즘 평가에 있어 성능평가에서 중요한 것은 worst case

Q. 평균적인 경우를 따져야 하는 것 아닌가?

A. 계산하는 것이 쉽지 않음. 다양한 이론 및 가정이 포함되어야 함. 아래의 average case 참고

순차 탐색 알고리즘 시간복잡도 : worst case

데이터 수가 n개일 때, 최악의 경우에 해당하는 연산횟수는 n

$\therefore T(n)=n$

순차 탐색 알고리즘 시간복잡도 : average case

평균적인 경우의 연산 횟수 계산을 위한 두가지 가정

• 가정 1. 탐색 대상이 배열에 존재하지 않을 확률이 50%
• 가정 2. 배열의 첫 요소부터 마지막 요소까지, 탐색 대상이 존재할 확률은 동일

case1. 배열에 탐색대상이 존재하지 않는 경우의 연산횟수

• 연산횟수 n

case2. 탐색 대상이 존재하는 경우의 연산횟수

• 연산횟수 n/2
  • 길이가 7인 배열의 경우, 위의 가정 2에 따라 각 배열요소에 탐색 대상이 존재할 확률이 동일하므로 7번 탐색하면, 연산 횟수가 1+2+3+4+5+6+7 = 28, 평균 28/7 = 4회
  • n/2 = 3.5회이지만, 근사치 계산 (수식이 간결해지고 배열의 길이가 길어질수록 근사치 계산결과에 가까워짐)
• 최종적으로는 가정 1에 따라, 1/2n + 1/2n/2 = 3/4*n
• 최악의 경우에 비해서 상대적으로 average case에 대한 시간복잡도를 구하기 쉽지 않고 신뢰도도 높지 않음
  • 앞서 2가지 가정을 뒷받침할 근거가 부족
  • 프로그램, 데이터 성격에 따라 배열에 탐색 대상이 존재할 확률이 50%가 아닐 수 있는데 이런 부분이 고려되지 않음

→ 결론 : Worst case를 시간 복잡도의 기준으로 삼는다

이진 탐색(Binary Search) 알고리즘의 소개

• 순차 탐색보다 높은 성능을 보이지만 아래의 조건을 만족해야 함
  • 배열에 저장된 데이터는 정렬되어 있어야 함

ex) 길이가 9인 배열

arr[] = {1, 2, 3, 7, 9, 12, 21, 23, 27};

이 배열을 대상으로 숫자 3이 저장되어 있는지 확인

첫번째 시도

• 배열 인덱스의 시작과 끝은 각각 0과 8
• 0과 8을 합하여 그 결과를 2로 나눔 → (0+8)/2 = 4
  • 2로 나눠서 얻은 결과 4를 인덱스 값으로 하여 arr[4]에 저장된 값이 3인지 확인 → NO

두번째 시도

• arr[4] 에 저장된 값 9와 탐색 대상인 3의 대소를 비교
  • arr[4] = 9
  • 찾고자 하는 대상 3
  • 배열이 오름차순으로 정렬되었음을 전제하였기 때문에 탐색 범위를 수정 가능
• arr[4] > 3이므로 탐색의 범위를 인덱스 기준 0~3으로 제한 (이전 : 0~8)
• 0과 3을 더하여 그 결과를 2로 나눔. 나머지는 버림. (0+3)/2 = 1.5 ⇒ 1
• 2로 나눠서 얻은 결과가 1이니, arr[1]에 저장된 값이 3인지 확인 → NO

→ 두번째 시도 만에 탐색의 대상을 반으로 줄임

세번째 시도

• arr[1]에서 저장된 값 2와 탐색 대상인 3의 대소를 비교
• 탐색 대상이 더 크므로 탐색의 범위를 인덱스 기준 2~3으로 제한(이전: 0~3)
• 2와 3을 더하여 그 결과를 2로 나눔. 나머지는 버림. (2+3)/2 = 2.5 → 2
• 2로 나눠서 얻은 결과가 2이니, arr[2]에 저장된 값이 3인지 확인 → YES

이진 탐색 알고리즘은 탐색의 대상을 반복하여 반씩 떨구어 내는 알고리즘

이진 탐색(Binary Search) 알고리즘의 구현

• 탐색의 시작 인덱스(first)와 마지막 인덱스(last) 값을 포함하는 범위로, 탐색의 범위를 반으로 줄여나감.

Q. 언제까지 계속되어야 하나?

A. first 와 last가 같아질 때까지? NO. 같아진 경우 하나의 탐색 범위가 있으므로 이때도 탐색해야 함

#include <iostream>
using namespace std;

int BSearch(int ar[], int len, int targetValue)
{
	int first = 0;      // 탐색 대상의 시작 인덱스 값
	int last = len - 1; // 탐색 대상의 마지막 인덱스 값
	int mid;

	while (first <= last) **// 중요(등호 포함됨)** 
	{
		mid = (first + last) / 2;

		if (targetValue == ar[mid])
		{
			return mid;
		}
		else //타겟이 아니라면 탐색 대상을 반으로 줄인다. 
		{
			if (targetValue < ar[mid])
				last = mid - 1; //왜 -1을 하였을까?
			else
				first = mid + 1; //왜 +1을 하였을까? 
		}
	}
	return -1;
}

int main()
{
	int arr[] = { 1,2,3,7,9,12,21,23,27 };
	int idx;

	idx = BSearch(arr, sizeof(arr) / sizeof(int), 7);
	if (idx == -1)
		cout << "탐색 실패" << endl;
	else
		cout << "타겟 저장 인덱스 : " << idx << endl;

	idx = BSearch(arr, sizeof(arr) / sizeof(int), 4);
	if (idx== -1)
		cout << "탐색 실패" << endl;
	else
		cout << "타겟 저장 인덱스 : " << idx << endl;

	return 0;
}

타겟 저장 인덱스 : 3 탐색 실패

Q. 위의 코드 중 while 문 조건에서 등호 (=)를 뺀 후 결과는?

탐색 실패 탐색 실패

• 값 7이 3번째 인덱스에 포함(arr[3] = 7)되어 있음에도 불구하고 탐색 실패의 결과를 얻음

→ "first가 last보다 큰 경우 탐색이 종료됨. 이렇게 종료되었다는 것은 탐색에 실패했음을 뜻함"

결론적으로 while문에서 '='를 빼면, worst case(탐색 범위가 하나만 남은 경우)에 index를 찾을 수 없게 됨

빅-오 표기법(Big-Oh Notation)

데이터의 수 n과 그에 따른 시간 복잡도 함수 T(n)을 정확히 그리고 오차 없이 구하는 것은 대부분의 경우 쉽지 않음

→ '빅-오'라는 것은 함수 T(n)에서 가장 영향력이 큰 부분이 어딘가를 따지는 것

ex) $T(n)=n^2+2n+1$ 은 $T(n)=n^2$ 로 간략화해서 진행할 수 있음

Q. 간략화 할 수 있는 이유는?

A. n의 값이 커질수록 T(n)에서 $n^2$이 차지하는 비율이 절대적으로 큼

표기는 $O(n^2)$로 하고, "빅-오 오브 n^2"로 읽음

단순하게 빅-오 구하기

"T(n)이 다항식으로 표현이 된 경우, 최고차항의 차수가 빅-오가 된다."

대표적인 빅-오

• $O(1)$ : 상수형 빅-오. 데이터 수에 상관없이 연산횟수가 고정인 유형의 알고리즘
• $O(logn)$ : 로그형 빅-오. '데이터 수의 증가율'에 비해서 '연산횟수의 증가율'이 훨씬 낮은 알고리즘
• $O(n)$ : 선형 빅-오. 데이터수와 연산횟수가 비례
• $O(nlogn)$ : 선형로그형 빅-오. 데이터의 수가 두배로 늘때, 연산횟수는 두배 조금 넘게 증가하는 알고리즘
• $O(n^2)$ : 데이터 수의 제곱에 해당하는 연산횟수를 요구하는 알고리즘→데이터 양이 많은 경우 적용하기 부적절
• $O(2^n)$ : 지수형 빅-오. 연산횟수가 지수적으로 증가

연산횟수 대소 정리

• $O(1) < O(logn)<O(n)<O(nlogn)<O(n^2)<O(2^n)$

순차 탐색 알고리즘과 이진 탐색 알고리즘의 비교

#include <iostream>
using namespace std;

//Linear search vs Binary search 비교

int BSearch(int ar[], int length, int targetValue)
{
	int first = 0;
	int last = length - 1;
	int mid;
	int opCount = 0; //비교연산의 횟수를 기록

	while (first <= last)
	{
		mid = (first + last) / 2;

		if (targetValue == ar[mid])
		{
			return mid;
		}
		else
		{
			if (targetValue < ar[mid])
				last = mid - 1;
			else
				first = mid + 1;
		}
		opCount += 1;
	}
	cout << "데이터 수 "<<length<<"에 대한 "<<"비교연산횟수 : " << opCount << endl;
	return -1;
}

int main()
{
	int arr1[500] = { 0, };
	int arr2[5000] = { 0, };
	int arr3[50000] = { 0, };
	int idx;

	//배열 arr1을 대상으로, 저장되지 않는 정수 1을 찾으라고 명령 
	idx = BSearch(arr1, sizeof(arr1) / sizeof(int), 1);
	if (idx == -1)
		cout << "탐색 실패" << endl;
	else
		cout << "타겟 저장 인덱스 : " << idx << endl;

	//배열 arr2을 대상으로, 저장되지 않는 정수 1을 찾으라고 명령 
	idx = BSearch(arr2, sizeof(arr2) / sizeof(int), 1);
	if (idx == -1)
		cout << "탐색 실패" << endl;
	else
		cout << "타겟 저장 인덱스 : " << idx << endl;

	//배열 arr1을 대상으로, 저장되지 않는 정수 1을 찾으라고 명령 
	idx = BSearch(arr3, sizeof(arr3) / sizeof(int), 1);
	if (idx == -1)
		cout << "탐색 실패" << endl;
	else
		cout << "타겟 저장 인덱스 : " << idx << endl;

	return 0;
}

데이터 수 500에 대한 비교연산횟수 : 9
탐색 실패
데이터 수 5000에 대한 비교연산횟수 : 13
탐색 실패
데이터 수 50000에 대한 비교연산횟수 : 16
탐색 실패

→ 순차 탐색 알고리즘의 Big Oh 가 O(n) 이므로, 비교해보면 $O(n)$ 과 $O(logn)$의 알고리즘 사이의 연산횟수에서 큰 차이를 보여줌