01-1 자료구조와 알고리즘
"프로그램이란 데이터를 표현하고, 그렇게 표현된 데이터를 처리하는 것이다"
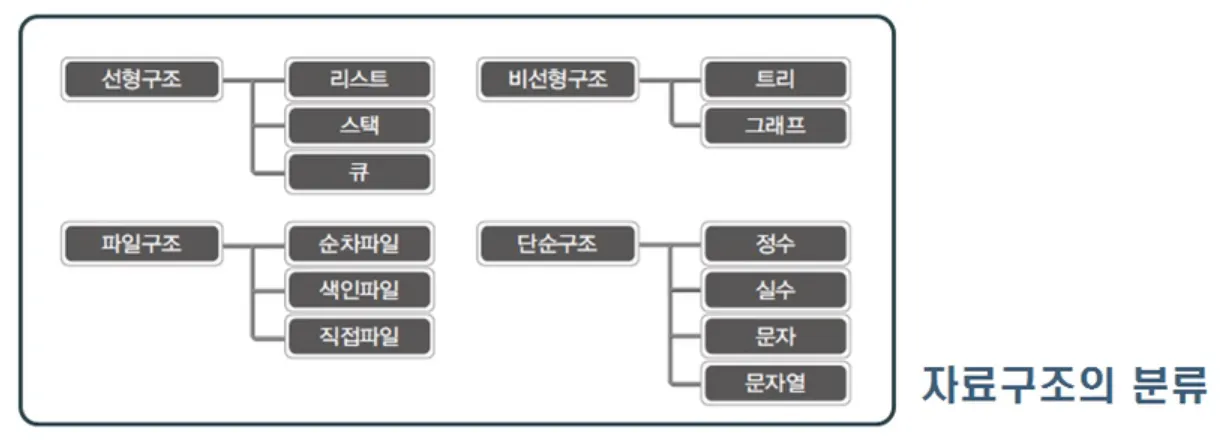
- 자료구조 : 데이터의 표현 및 저장방법
- 알고리즘 : 표현 및 저장된 데이터를 대상으로 하는 '문제의 해결 방법'
→ 자료구조에 따라서 알고리즘은 달라지고, 알고리즘은 자료구조에 의존적
01-2 알고리즘의 성능분석 방법
시간 복잡도(Time complexity)와 공간 복잡도(Space complexity)
- 잘 동작하는 것에 더하여 좋은 성능을 보장하기 위해 자료구조와 알고리즘을 분석하고 평가할 수 있어야 함 (만능은 존재하지 않음)
- 시간복잡도 : 속도에 해당하는 알고리즘의 수행시간 분석 결과 (cpu에 얼마나 부하를 주는가?)
- 공간복잡도 : 메모리 사용량에 대한 분석 결과
일반적으로 알고리즘을 평가할 때 메모리의 사용량보다 실행속도에 초점을 둠. 공간복잡도는 보조적인 역할
Q. 어떻게 속도를 평가하나?
- 특정 상황에 대해서 속도를 재는 것은 무의미
- $\because$ 처리해야 할 데이터 양의 변화에 따라 속도의 증가 및 감소의 정도가 달라지기 때문
- 위의 이유로 알고리즘의 수행속도를 평가할 때 다음과 같은 방식을 취함
- 연산의 횟수를 셈
- 처리해야 할 데이터의 수 n에 대한 연산횟수의 함수 T(n)을 구성
- 식을 구성하면 데이터 수의 증가에 따른 연산횟수의 변화 정도를 판단할 수 있고, 다른 알고리즘들의 시간복잡도를 비교할 수 있음

알고리즘은 상황에 맞게 종합적으로 사고하고 판단하여 선택해야 함
- 데이터의 수가 많아짐에 따른 연산횟수의 증가 정도가 중요하므로 알고리즘 A가 B보다 훨씬 좋은 알고리즘. T(n)함수에 대한 패턴이 중요함
- 그렇다고 알고리즘 B가 필요없는게 아님
- B와 같은 성격의 알고리즘은 A보다 구현이 쉬워 데이터의 수가 많지 않고 성능에 덜 민감한 경우라면 구현의 편의를 위해 B를 선택하기도 함
순차 탐색(Linear Search) 알고리즘과 시간 복잡도 분석의 핵심요소
#include<iostream>
using namespace std;
int LSearch(int ar[], int len, int target) // 순차 탐색 알고리즘 적용된 함수
{
int i;
for (i = 0; i < len; i++)
{
if (ar[i] == target)
return i; //찾은 대상의 인덱스 값 반환
}
return -1;
}
int main(void)
{
int arr[] = { 3, 5, 2, 4, 9 };
int idx;
idx = LSearch(arr, sizeof(arr) / sizeof(int), 4);
if (idx == -1)
cout<<"탐색 실패"<<endl;
else
cout<<"타겟 저장 인덱스 : "<<idx<<endl;
idx = LSearch(arr, sizeof(arr) / sizeof(int), 7);
if (idx == 01)
cout<<"탐색 실패"<<endl;
else
cout<<"타겟 저장 인덱스 : "<<idx<<endl;
return 0;
}타겟 저장 인덱스 : 3
타겟 저장 인덱스 : -1
- 좋은 탐색 알고리즘에서는 비교하는 '==' 연산이 적게 수행되어야 함
- '<'와 '++'는 '=='연산자가 true를 반환할 때까지 수행이 됨
최악의 경우와 최상의 경우
- 탐색의 대상이 되는 요소의 수(ex) 배열길이)가 n인 경우,
- 운이 좋아서 찾고자 하는 값이 배열의 맨 앞에 저장된 경우, 연산 횟수 1회 (best case)
- 운이 없어서 찾고자 하는 값이 배열의 맨 뒤에 저장된 경우, 연산 횟수 n회 (worst case)
- 알고리즘 평가에 있어 성능평가에서 중요한 것은 worst case
Q. 평균적인 경우를 따져야 하는 것 아닌가?
A. 계산하는 것이 쉽지 않음. 다양한 이론 및 가정이 포함되어야 함. 아래의 average case 참고
순차 탐색 알고리즘 시간복잡도 : worst case
데이터 수가 n개일 때, 최악의 경우에 해당하는 연산횟수는 n
$\therefore T(n)=n$
순차 탐색 알고리즘 시간복잡도 : average case
평균적인 경우의 연산 횟수 계산을 위한 두가지 가정
- 가정 1. 탐색 대상이 배열에 존재하지 않을 확률이 50%
- 가정 2. 배열의 첫 요소부터 마지막 요소까지, 탐색 대상이 존재할 확률은 동일
case1. 배열에 탐색대상이 존재하지 않는 경우의 연산횟수
- 연산횟수 n
case2. 탐색 대상이 존재하는 경우의 연산횟수
- 연산횟수 n/2
- 길이가 7인 배열의 경우, 위의 가정 2에 따라 각 배열요소에 탐색 대상이 존재할 확률이 동일하므로 7번 탐색하면, 연산 횟수가 1+2+3+4+5+6+7 = 28, 평균 28/7 = 4회
- n/2 = 3.5회이지만, 근사치 계산 (수식이 간결해지고 배열의 길이가 길어질수록 근사치 계산결과에 가까워짐)
- 최종적으로는 가정 1에 따라, 1/2n + 1/2n/2 = 3/4*n
- 최악의 경우에 비해서 상대적으로 average case에 대한 시간복잡도를 구하기 쉽지 않고 신뢰도도 높지 않음
- 앞서 2가지 가정을 뒷받침할 근거가 부족
- 프로그램, 데이터 성격에 따라 배열에 탐색 대상이 존재할 확률이 50%가 아닐 수 있는데 이런 부분이 고려되지 않음
→ 결론 : Worst case를 시간 복잡도의 기준으로 삼는다
이진 탐색(Binary Search) 알고리즘의 소개
- 순차 탐색보다 높은 성능을 보이지만 아래의 조건을 만족해야 함
- 배열에 저장된 데이터는 정렬되어 있어야 함
ex) 길이가 9인 배열
arr[] = {1, 2, 3, 7, 9, 12, 21, 23, 27};
이 배열을 대상으로 숫자 3이 저장되어 있는지 확인
첫번째 시도
- 배열 인덱스의 시작과 끝은 각각 0과 8
- 0과 8을 합하여 그 결과를 2로 나눔 → (0+8)/2 = 4
- 2로 나눠서 얻은 결과 4를 인덱스 값으로 하여 arr[4]에 저장된 값이 3인지 확인 → NO

두번째 시도
- arr[4] 에 저장된 값 9와 탐색 대상인 3의 대소를 비교
- arr[4] = 9
- 찾고자 하는 대상 3
- 배열이 오름차순으로 정렬되었음을 전제하였기 때문에 탐색 범위를 수정 가능
- arr[4] > 3이므로 탐색의 범위를 인덱스 기준 0~3으로 제한 (이전 : 0~8)
- 0과 3을 더하여 그 결과를 2로 나눔. 나머지는 버림. (0+3)/2 = 1.5 ⇒ 1
- 2로 나눠서 얻은 결과가 1이니, arr[1]에 저장된 값이 3인지 확인 → NO
→ 두번째 시도 만에 탐색의 대상을 반으로 줄임

세번째 시도
- arr[1]에서 저장된 값 2와 탐색 대상인 3의 대소를 비교
- 탐색 대상이 더 크므로 탐색의 범위를 인덱스 기준 2~3으로 제한(이전: 0~3)
- 2와 3을 더하여 그 결과를 2로 나눔. 나머지는 버림. (2+3)/2 = 2.5 → 2
- 2로 나눠서 얻은 결과가 2이니, arr[2]에 저장된 값이 3인지 확인 → YES

이진 탐색 알고리즘은 탐색의 대상을 반복하여 반씩 떨구어 내는 알고리즘
이진 탐색(Binary Search) 알고리즘의 구현
- 탐색의 시작 인덱스(first)와 마지막 인덱스(last) 값을 포함하는 범위로, 탐색의 범위를 반으로 줄여나감.
Q. 언제까지 계속되어야 하나?
A. first 와 last가 같아질 때까지? NO. 같아진 경우 하나의 탐색 범위가 있으므로 이때도 탐색해야 함
#include <iostream>
using namespace std;
int BSearch(int ar[], int len, int targetValue)
{
int first = 0; // 탐색 대상의 시작 인덱스 값
int last = len - 1; // 탐색 대상의 마지막 인덱스 값
int mid;
while (first <= last) **// 중요(등호 포함됨)**
{
mid = (first + last) / 2;
if (targetValue == ar[mid])
{
return mid;
}
else //타겟이 아니라면 탐색 대상을 반으로 줄인다.
{
if (targetValue < ar[mid])
last = mid - 1; //왜 -1을 하였을까?
else
first = mid + 1; //왜 +1을 하였을까?
}
}
return -1;
}
int main()
{
int arr[] = { 1,2,3,7,9,12,21,23,27 };
int idx;
idx = BSearch(arr, sizeof(arr) / sizeof(int), 7);
if (idx == -1)
cout << "탐색 실패" << endl;
else
cout << "타겟 저장 인덱스 : " << idx << endl;
idx = BSearch(arr, sizeof(arr) / sizeof(int), 4);
if (idx== -1)
cout << "탐색 실패" << endl;
else
cout << "타겟 저장 인덱스 : " << idx << endl;
return 0;
}타겟 저장 인덱스 : 3 탐색 실패
Q. 위의 코드 중 while 문 조건에서 등호 (=)를 뺀 후 결과는?
탐색 실패 탐색 실패
- 값 7이 3번째 인덱스에 포함(arr[3] = 7)되어 있음에도 불구하고 탐색 실패의 결과를 얻음
→ "first가 last보다 큰 경우 탐색이 종료됨. 이렇게 종료되었다는 것은 탐색에 실패했음을 뜻함"
결론적으로 while문에서 '='를 빼면, worst case(탐색 범위가 하나만 남은 경우)에 index를 찾을 수 없게 됨
빅-오 표기법(Big-Oh Notation)
데이터의 수 n과 그에 따른 시간 복잡도 함수 T(n)을 정확히 그리고 오차 없이 구하는 것은 대부분의 경우 쉽지 않음
→ '빅-오'라는 것은 함수 T(n)에서 가장 영향력이 큰 부분이 어딘가를 따지는 것
ex) $T(n)=n^2+2n+1$ 은 $T(n)=n^2$ 로 간략화해서 진행할 수 있음
Q. 간략화 할 수 있는 이유는?
A. n의 값이 커질수록 T(n)에서 $n^2$이 차지하는 비율이 절대적으로 큼
표기는 $O(n^2)$로 하고, "빅-오 오브 n^2"로 읽음
단순하게 빅-오 구하기
"T(n)이 다항식으로 표현이 된 경우, 최고차항의 차수가 빅-오가 된다."
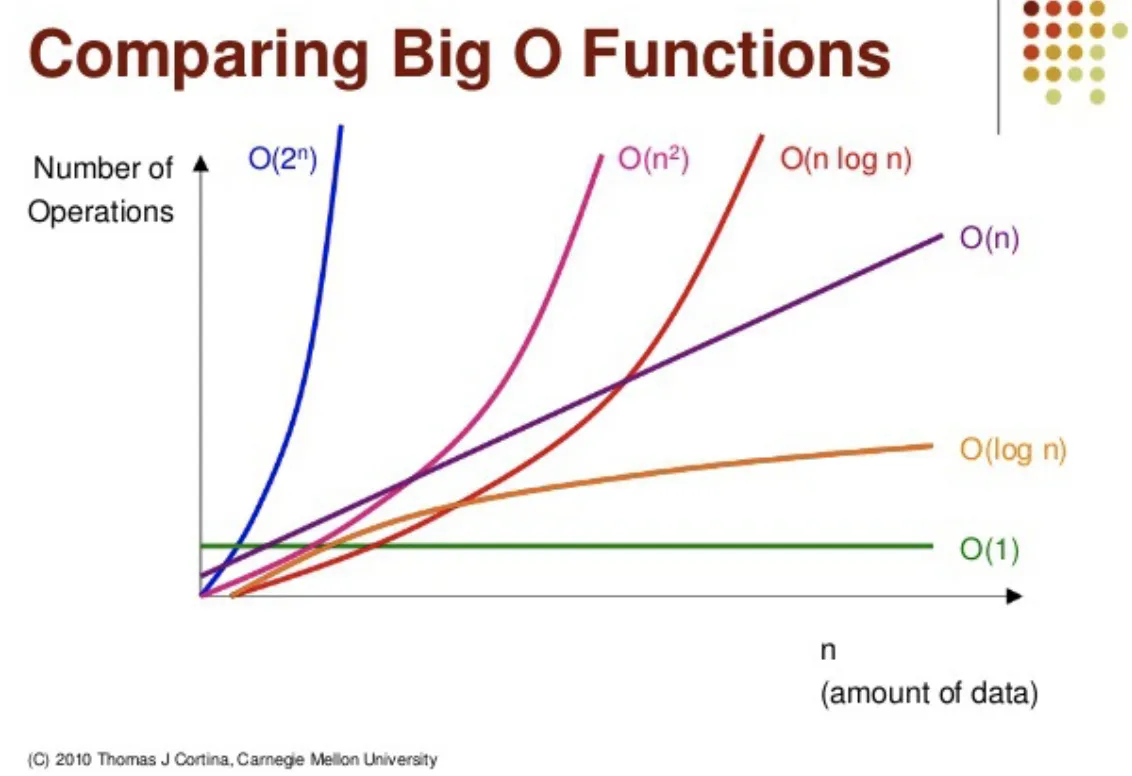
대표적인 빅-오
- $O(1)$ : 상수형 빅-오. 데이터 수에 상관없이 연산횟수가 고정인 유형의 알고리즘
- $O(logn)$ : 로그형 빅-오. '데이터 수의 증가율'에 비해서 '연산횟수의 증가율'이 훨씬 낮은 알고리즘
- $O(n)$ : 선형 빅-오. 데이터수와 연산횟수가 비례
- $O(nlogn)$ : 선형로그형 빅-오. 데이터의 수가 두배로 늘때, 연산횟수는 두배 조금 넘게 증가하는 알고리즘
- $O(n^2)$ : 데이터 수의 제곱에 해당하는 연산횟수를 요구하는 알고리즘→데이터 양이 많은 경우 적용하기 부적절
- $O(2^n)$ : 지수형 빅-오. 연산횟수가 지수적으로 증가
연산횟수 대소 정리
- $O(1) < O(logn)<O(n)<O(nlogn)<O(n^2)<O(2^n)$
순차 탐색 알고리즘과 이진 탐색 알고리즘의 비교
#include <iostream>
using namespace std;
//Linear search vs Binary search 비교
int BSearch(int ar[], int length, int targetValue)
{
int first = 0;
int last = length - 1;
int mid;
int opCount = 0; //비교연산의 횟수를 기록
while (first <= last)
{
mid = (first + last) / 2;
if (targetValue == ar[mid])
{
return mid;
}
else
{
if (targetValue < ar[mid])
last = mid - 1;
else
first = mid + 1;
}
opCount += 1;
}
cout << "데이터 수 "<<length<<"에 대한 "<<"비교연산횟수 : " << opCount << endl;
return -1;
}
int main()
{
int arr1[500] = { 0, };
int arr2[5000] = { 0, };
int arr3[50000] = { 0, };
int idx;
//배열 arr1을 대상으로, 저장되지 않는 정수 1을 찾으라고 명령
idx = BSearch(arr1, sizeof(arr1) / sizeof(int), 1);
if (idx == -1)
cout << "탐색 실패" << endl;
else
cout << "타겟 저장 인덱스 : " << idx << endl;
//배열 arr2을 대상으로, 저장되지 않는 정수 1을 찾으라고 명령
idx = BSearch(arr2, sizeof(arr2) / sizeof(int), 1);
if (idx == -1)
cout << "탐색 실패" << endl;
else
cout << "타겟 저장 인덱스 : " << idx << endl;
//배열 arr1을 대상으로, 저장되지 않는 정수 1을 찾으라고 명령
idx = BSearch(arr3, sizeof(arr3) / sizeof(int), 1);
if (idx == -1)
cout << "탐색 실패" << endl;
else
cout << "타겟 저장 인덱스 : " << idx << endl;
return 0;
}데이터 수 500에 대한 비교연산횟수 : 9
탐색 실패
데이터 수 5000에 대한 비교연산횟수 : 13
탐색 실패
데이터 수 50000에 대한 비교연산횟수 : 16
탐색 실패
→ 순차 탐색 알고리즘의 Big Oh 가 O(n) 이므로, 비교해보면 $O(n)$ 과 $O(logn)$의 알고리즘 사이의 연산횟수에서 큰 차이를 보여줌
'자료구조' 카테고리의 다른 글
| [책리뷰] 윤성우의 열혈 자료구조 Ch3. Linked list 1 - 배열기반 (0) | 2024.10.27 |
|---|---|
| [책리뷰] 윤성우의 열혈 자료구조 Ch2. 재귀 (0) | 2024.10.27 |
| [자료구조] Stack (0) | 2022.10.04 |
| [자료구조] Linked List - (6) 노드 삭제 (0) | 2022.06.12 |
| [자료구조] Linked List - (5) 데이터 조회 (0) | 2022.06.12 |